リモートセンシングによる海草マッピングの最も重要なテーマの一つは、分類の精度評価です。 一般に、分類の精度は誤差行列 (混同行列または分割表) を使用して評価されます (Mumby and Green 2000)。 精度は、ユーザーの精度、作成者の精度、全体の精度、およびタウ係数によって判断されます (Ma and Redmond 1995)。
1. エラー マトリックス (ピクセルとパーセント)
誤差は、各グラウンド トゥルース ピクセルのクラスを分類画像内の対応するクラスと比較することによって計算されます。 誤差行列の各列はグラウンド トゥルース クラスを表し、列内の値は分類画像のグラウンド トゥルース ピクセルのラベル付けに対応します。 表 3 は、各グラウンド トゥルース クラスのピクセル単位のクラス分布とパーセンテージを示しています。
ユーザー精度は、分類器が画像ピクセルをクラス A にラベル付けした場合に、ピクセルがクラス A である確率を示す尺度です。ユーザー精度は誤差行列の行に示されます。 たとえば、表 3 では、地上調査で取得された海草ピクセルは 50 個あり、そのうち 39 個と 11 個がそれぞれ正しく分類され、誤って分類されています。 海草クラスに正しく分類されたピクセル数と誤って分類されたピクセル数の割合は、それぞれ 78% と 22% (表 3) であり、ユーザーの正確さと委託の誤差に対応します。
プロデューサーの精度は、グラウンド トゥルースがクラス A であると仮定して、分類子が画像ピクセルをクラス A にラベル付けした確率を示す尺度です。たとえば、表 3 では、グラウンド トゥルースの海草クラスには合計 48 ピクセルがあり、そのうち 39 ピクセルが含まれています。および 9 ピクセルはそれぞれ正しく分類され、81.3 ピクセルは誤って分類されます。 地上調査で得られた海草ピクセル数の正確な分類と誤った分類の割合は、それぞれ 18.8% と 1% (表 XNUMX) であり、生産者の精度と省略の誤差に相当します。
全体的な精度は、正しく分類されたピクセル数を合計し、ピクセルの総数で割ることによって計算されます。 正しく分類されたピクセルは、正しいグラウンド トゥルース クラスに分類されたピクセルの数をリストするエラー マトリックス テーブルの対角線に沿って見つかります。 ピクセルの合計数は、すべてのグラウンド トゥルース クラスのすべてのピクセルの合計です。 たとえば、表 3 では、対角成分のピクセル数は海草の 39 ピクセルと砂の 51 ピクセルで構成されており、これらは正しく分類されたピクセルです。 全体的な精度 (81.8%) は、正しく分類されたピクセル数 (39+51) をグラウンド トゥルース ピクセルの総数 (110) で割ることによって得られます。
全体的な精度は、マトリックス内の全体的な一致度です。 一般に、沿岸海底の表面被覆の分類の精度は、陸上の表面被覆の精度よりも低くなります(例 Mumby et al., 1998)。 Mumby et al. (1999) は、LANDSAT TM などの衛星画像または SPOT を使用した LANDSAT TM のパンシャープン画像を使用することにより、サンゴ/海草やマングローブ/非マングローブなどの粗い記述解像度の妥当な精度が 60 ~ 80% であると述べています。 いずれの場合でも、リモートセンシングを使用して底カバーの空間分布の時間的変化を監視するための全体的な精度は約 90% 以上です (Mumby and Green、2000)。
2.タウ係数
これはマップの全体的な精度を説明する合理的な方法ですが、偶然のみから生じる精度の要素は考慮されていません。 ピクセルを生息地クラスにランダムに割り当てた場合でも、正しい割り当てが含まれるため、精度には偶然の要素が存在します。
タウ係数 T(e) は、偶然の成分を除外するための分類の精度のもう XNUMX つの尺度であり、次の方程式で表されます。
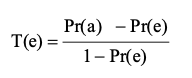
ここで、Pr(a) と Pr(e) は、クラス間で観察された相対的な一致と偶然の一致の仮説確率です。 たとえば、表 3 では、Pr(a) は全体の精度 0.818 に対応します。 0.5 つのクラスから導出された Pr(e) は 0.636 です。 次に、(0.818-0.50) を (1.0-0.5) で割ることにより、T(e) が 1.0 として得られます。 タウ係数の範囲は -1.0 ~ 1.0 です。 タウ係数が -1.0 と 0.41 の場合、分類はそれぞれ完全に一致し、完全に一致します。 タウが 0.60 ~ 0.61 の場合、分類は中程度の一致を示します。 タウが 0.80 ~ 0.80 の場合、分類はよく一致します。 タウが XNUMX を超える場合、分類はほぼ完全に一致します。
タウの分散、σ2、次の方程式として計算されます (Ma and Redmond 1995)。
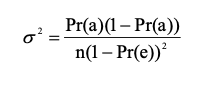
ここで、n はサンプルの数です。 次に、次の形式を使用して、95% 信頼水準 (1-α) で各タウ係数の信頼区間が計算されます。
![]()
コラボレー Z は、下限が α/2 の標準正規分布です。 表 3 を使用すると、95% CI が 0.636 ±0.001 として得られます。 係数の分布は正規性に近似し、Z 検定を実行して行列間の差異を調べることができます (Ma and Redmond 1995)。 1 つの異なる分類方法 (方法 2 と方法 XNUMX) が適用される場合、Z 検定を実行して、タウ係数に有意な差があるかどうかを検証します (T1 および T2) 方法 1 と方法 2 で得られた結果の間に存在するかどうかは、次の式を使用して計算されます。
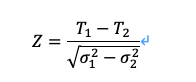
ここで、σ2 は、式 (10) から計算されたタウ係数の分散です。 タウ係数が 95% の確率で異なるかどうかを調べることができます。